栈
一、栈
1、栈的介绍
1. 栈的英文为(stack)
2. 栈是一个先入后出(FILO-FirstInLastOut)的有序列表。
3. 栈(stack)是限制线性表中元素的插入和删除只能在线性表的同一端进行的一种特殊线性表。允许插入和删除的 一端,为变化的一端,称为栈顶(Top),另一端为固定的一端,称为栈底(Bottom)。
4. 根据栈的定义可知,最先放入栈中元素在栈底,最后放入的元素在栈顶,而删除元素刚好相反,最后放入的元素最先删除,最先放入的元素最后删除
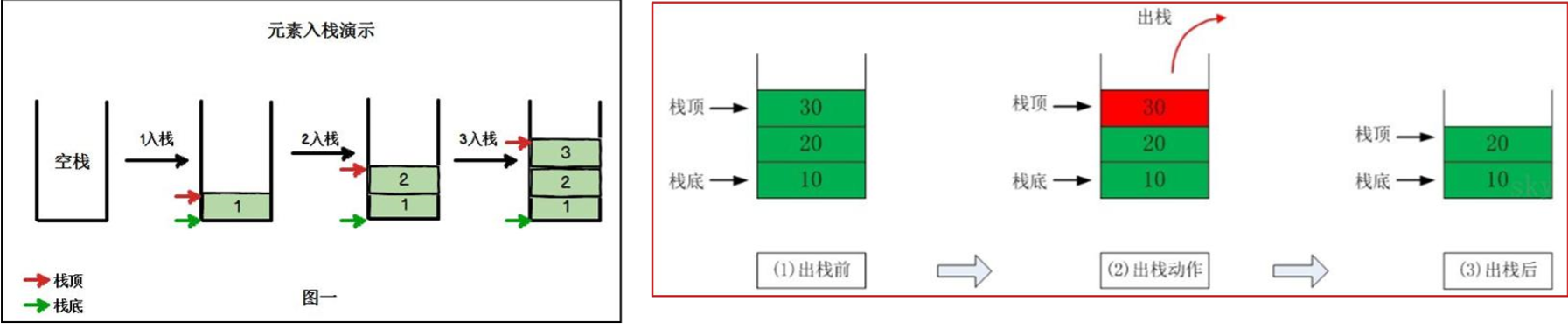
5. 图解方式说明出栈(pop)和入栈(push)的概念------------------------------>
2、栈的应用场景
1. 子程序的调用:在跳往子程序前,会先将下个指令的地址存到堆栈中,直到子程序执行完后再将地址取出,以回到原来的程序中。
2. 处理递归调用:和子程序的调用类似,只是除了储存下一个指令的地址外,也将参数、区域变量等数据存入堆栈中。
3. 表达式的转换[中缀表达式转后缀表达式]与求值(实际解决)。
4. 二叉树的遍历。
5. 图形的深度优先(depth 一 first)搜索法。
3、栈代码实现和思路分析
1. 使用数组来模拟栈
2. 定义一个变量为 top ,来表示栈顶,初始化为 -1
3. 入栈的操作:当有数据加入到栈式, top++; stack[top] = data
4. 出栈的操作:int value = stack[top]; top --; return value;
二、栈代码实现
package com.yixuexi.stack;
import java.util.ArrayList;
/**
* 2020/10/13 17:19
*/
//使用数组模拟栈
public class ArrayStackDemo {
public static void main(String[] args) {
ArrayStack arrayStack = new ArrayStack(5);
arrayStack.push(1);
arrayStack.push(2);
arrayStack.push(3);
arrayStack.push(4);
arrayStack.push(5);
arrayStack.showStack();
int pop = arrayStack.pop();
System.out.println("弹出的为:" + pop);
arrayStack.showStack();
}
}
class ArrayStack{
public int maxSize; //表示栈能储存的元素
public int top = -1; //表示栈顶
public int[] stack;//模拟栈
public ArrayStack(int maxSize){
this.maxSize = maxSize;
stack = new int[maxSize];
}
//判断栈是否已满
public boolean isFull(){
return top == maxSize-1;
}
//判断栈是不是空
public boolean isEmpty(){
return top == -1;
}
//弹栈
public int pop(){
//首先判断栈是不是为空,如果为空的话那么就没必要弹栈了
if (isEmpty()){
throw new RuntimeException("栈为空,无法弹栈");
}
//得到弹出来的数据
int value = stack[top];
top --;
return value;
}
//入栈
public void push(int value){
//首先判断栈是不是满了,如果满了那么就无法进行压栈了
if (isFull()){
System.out.println("栈以满!无法入栈");
return;
}
top ++;
stack[top] = value;
}
//展示栈中的数据
public void showStack(){
//要从给栈的顶部往下展示,因为是栈
//判断栈是不是为空,如果为空没必要进行展示
if (isEmpty()){
System.out.println("栈为空");
return;
}
for (int i = top; i >= 0; i--){
System.out.println(stack[i]);
}
}
}
三、栈完成数学表达式
1、思路:
1. 通过一个 index值 来遍历 数学表达式
2. 如果发现是一个数字,就直接压入数字栈 (需要两个栈,一个 数组栈,一个符号栈)
3. 如果发现是一个符号,就分以下情况:
a. 如果发现当前的符号栈为空,就直接入栈。
b. 如果符号栈中有操作符,就进行比较,如果当前的操作符的优先级小于或者等于栈中的操作符 就需要从数字栈中pop出两个数字,在从符号栈中pop出一个符号,进行运算,将得到结果,入数栈,然后将当前的操作符号入符号栈,如果当前的操作符的优先级大于栈中的操作符,就直接入符号栈。
4. 当表达式扫描完毕,就顺序的从数栈和符号栈中pop出相应的数字和符号,并运行
5. 最后在数栈只有一个数字,就是表达式的结果
四、递归
1. 看一个实际应用场景,迷宫问题(回溯),递归
2. 递归简单的来说:有一个方法 自己调用自己,每次调用时传入不同的变量,递归有助于编程者解决复杂的问题,同时让代码变得简洁。
3. 递归小题(打印问题 / 阶乘问题)
public class Test01 {
public static void main(String[] args) {
//打印问题
test(9);
//阶乘问题
System.out.println(jc(5));
}
//打印问题 从2 打印到 n
public static void test(int n){
if(n > 2){
test(n - 1);
}
System.out.println("n = "+ n);
}
//阶乘
public static long jc(long n){
if(n == 1){
return 1;
}else{
return jc(n-1)*n;
}
}
}
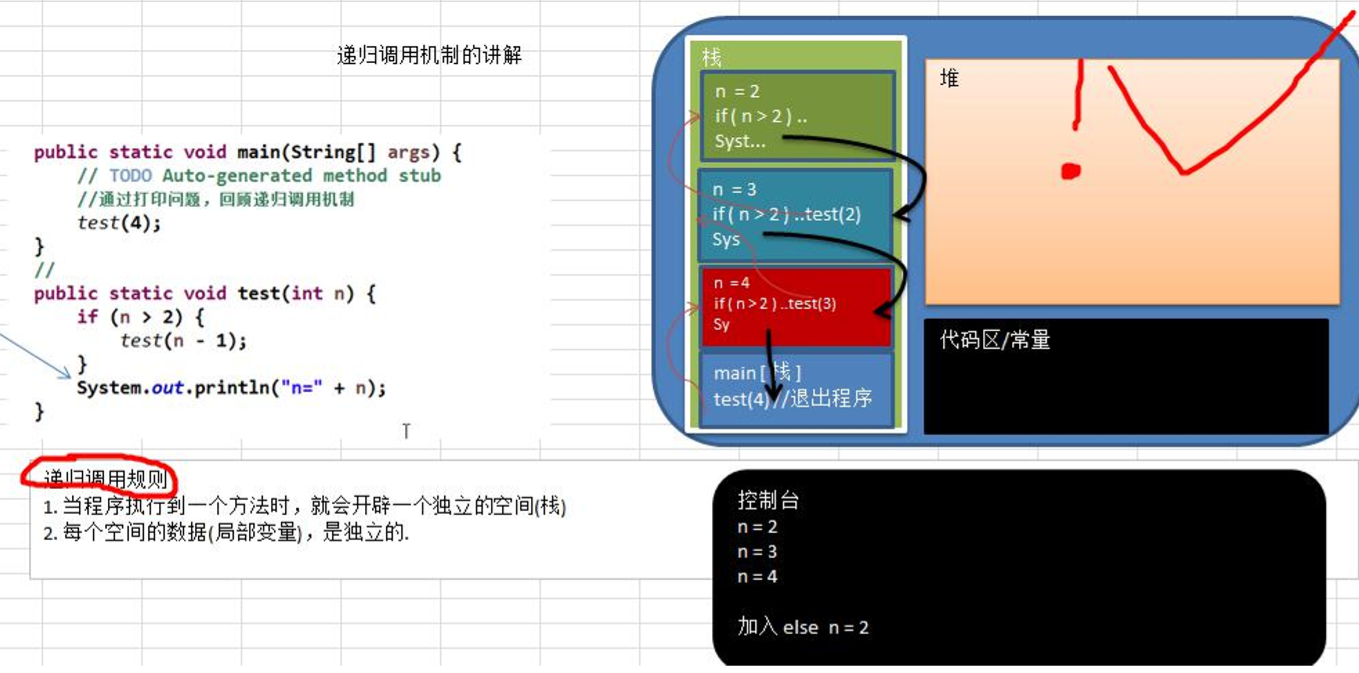
1. 递归调用机制
a. 当程序执行到一个方法时,就会开辟一个独立的空间(栈)
b. 每个空间的数据(局部变量是独立的)
2. 递归能解决什么样的问题:
a. 各种数学问题:8皇后问题,汉诺塔,阶乘问题,迷宫问题,球和篮子的问题
b. 各种算法中也会使用到递归, 比如快速排序,归并排序,二分查找,分治算法
3. 递归需要遵守的重要规则
a. 执行一个方法时,就创建一个新的受保护的独立空间(栈空间)
b. 方法的局部变量是独立的,不会互相影响
c. 如果方法中使用的引用类型的数据(数组..),就会共享该引用类型的数据。
d. 递归必须向退出递归的条件逼近,否则就是无限递归,死龟了,出现stackOverflowError错误
e. 当一个方法执行完毕,或者遇到return 就会返回,遵守谁调用,就将结果返回给谁,同时当方法执行完毕或者返回时,该方法也就执行完毕。